Proving De Gua’s theorem with Clifford algebra
by Stéphane Haussler
I just watched yet another great video by Michael Penn about De Gua’s theorem. Since I had never heard
of it and recently learned about Clifford Algebra as well as the Hodge dual, I
decided I would have a go at it that way. It felt a proof should work out
nicely, and it does!
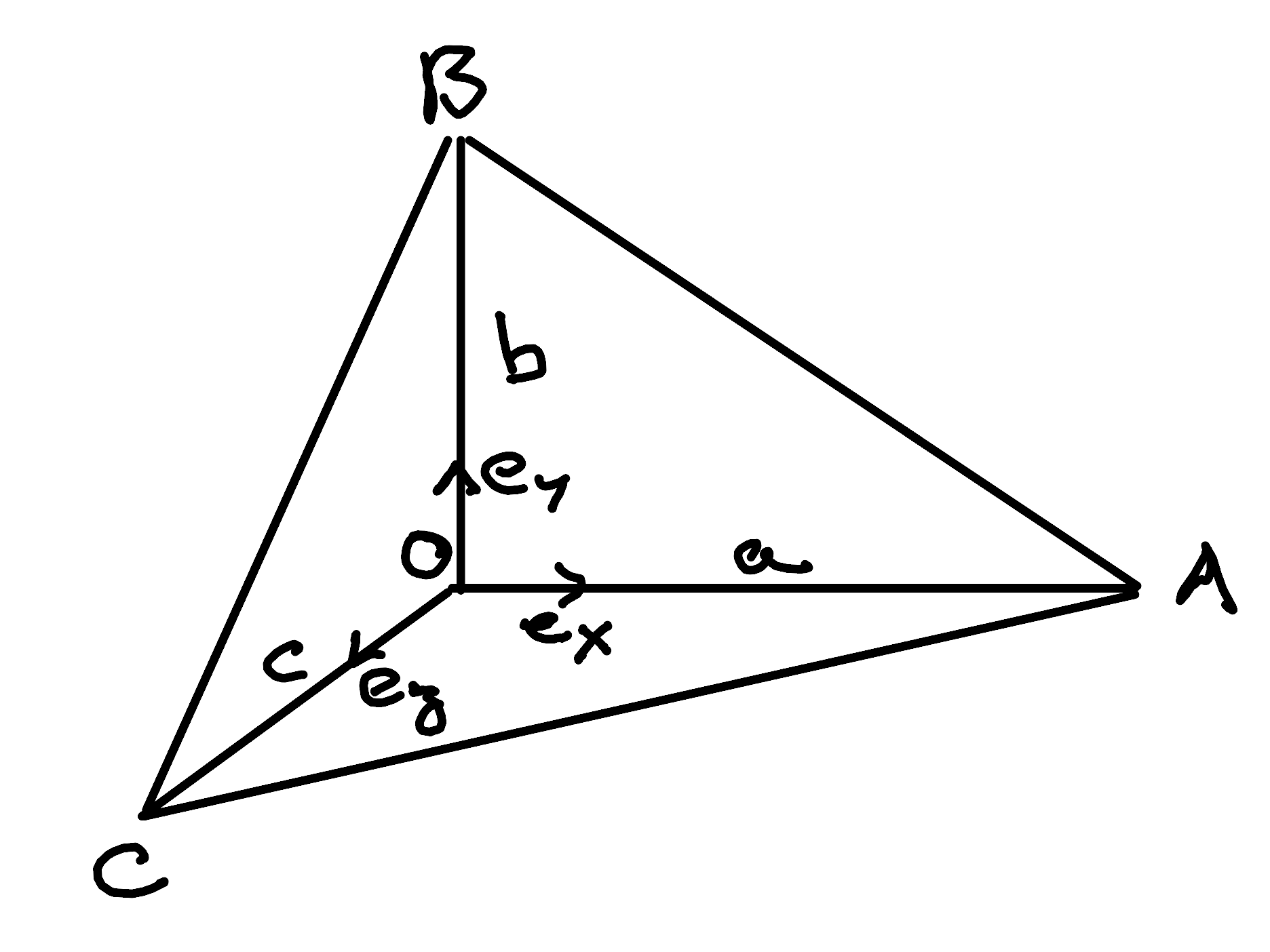
The theorem states that with an orthogonal corner \(O\) and triangles
arranged as shown in the illustration, their areas follows this rule:
\[A^2_{ABC} = A^2_{OBC} + A^2_{OAC} + A^2_{OAB}\]
Don’t hesitate to open an issue in the Theoretical Universe repository if something is not
as it should. You can also correct directly and I will definitely conside
merging your changes.
Taking the Clifford Product
Take the Clifford product of vectors \(\mathbf{CA}\) and
\(\mathbf{CB}\):
\[\begin{split}\mathbf{CA\;CB} &= (\mathbf{CO + OA}) (\mathbf{CO + OB}) \\
&= \mathbf{CO\;CO} + \mathbf{CO\;OB} + \mathbf{OA\;CO} + \mathbf{OA\;OB} \\\end{split}\]
Expand the Cifford product on both sides into dot and wedge products:
\[\begin{split}\mathbf{CA} \cdot \mathbf{CB} + \mathbf{CA} \wedge \mathbf{CB}
= & \mathbf{CO} \cdot \mathbf{CO} + \mathbf{CO} \wedge \mathbf{CO} + \\
& \mathbf{CO} \cdot \mathbf{OB} + \mathbf{CO} \wedge \mathbf{OB} + \\
& \mathbf{OA} \cdot \mathbf{CO} + \mathbf{OA} \wedge \mathbf{CO} + \\
& \mathbf{OA} \cdot \mathbf{OB} + \mathbf{OA} \wedge \mathbf{OB} + \\\end{split}\]
\(\mathbf{CO}\) is aligned with itself and its wedge product is therefore
zero (its dot product is not zero). Since we make the hypothesis of a right
corner in \(O\), all other dot products are zero.
\[\begin{split}\mathbf{CA} \cdot \mathbf{CB} + \mathbf{CA} \wedge \mathbf{CB} =
& + \mathbf{CO} \cdot \mathbf{CO} \\
& + \mathbf{CO} \wedge \mathbf{OB} \\
& + \mathbf{OA} \wedge \mathbf{CO} \\
& + \mathbf{OA} \wedge \mathbf{OB} \\\end{split}\]
Identifying the Bivector Part
Isolate the bivector part:
\[\begin{split}\mathbf{CA} \wedge \mathbf{CB} =
\mathbf{CO} \wedge \mathbf{OB} + \mathbf{OA} \wedge \mathbf{CO} + \mathbf{OA} \wedge \mathbf{OB} \\\end{split}\]
With reference to the illustration, we use the area \(A\) and basis vectors
\(\mathbf{e}_i\):
\[\mathbf{CA} \wedge \mathbf{CB} =
- A_{OCB} \; \mathbf{e_z} \wedge \mathbf{e_y}
- A_{OAC} \; \mathbf{e_x} \wedge \mathbf{e_z}
+ A_{OAB} \; \mathbf{e_x} \wedge \mathbf{e_y}\]
Reorder:
\[\mathbf{CA} \wedge \mathbf{CB} =
+ A_{OCB} \; \mathbf{e_y} \wedge \mathbf{e_z}
+ A_{OAC} \; \mathbf{e_z} \wedge \mathbf{e_x}
+ A_{OAB} \; \mathbf{e_x} \wedge \mathbf{e_y}\]
Taking the Hodge Dual
Take the Hodge dual of that last expression:
\[\star \mathbf{CA} \wedge \mathbf{CB} =
+ A_{OCB} \; \star \mathbf{e_y} \wedge \mathbf{e_z}
+ A_{OAC} \; \star \mathbf{e_z} \wedge \mathbf{e_x}
+ A_{OAB} \; \star \mathbf{e_x} \wedge \mathbf{e_y}\]
Which results in:
\[\mathbf{CA} \times \mathbf{CB} =
+ A_{OCB} \; \mathbf{e_x}
+ A_{OAC} \; \mathbf{e_y}
+ A_{OAB} \; \mathbf{e_z}\]
Consider the unit vector \(\mathbf{n}\) normal to the \(ABC\) surface.
\[A_{ABC} \; \mathbf{n} =
+ A_{OCB} \; \mathbf{e_x}
+ A_{OAC} \; \mathbf{e_y}
+ A_{OAB} \; \mathbf{e_z}\]
Taking the squared norm and obtain De Gua’s theorem:
\[A^2_{ABC} = A^2_{OBC} + A^2_{OAC} + A^2_{OAB}\]
